Gottlob Frege

2.1. Early Life and Education

Friedrich Ludwig Gottlob Frege was born on November 8, 1848, in Wismar, then part of the Grand Duchy of Mecklenburg-Schwerin, which was officially under the Swedish-Norwegian Empire but de facto German-controlled, and eventually returned to Mecklenburg in 1908. His father, Carl (Karl) Alexander Frege (1809-1866), was a co-founder and headmaster of a girls' high school. Carl Alexander also authored a German language textbook for children aged 9 to 13, titled Hülfsbuch zum Unterrichte in der deutschen Sprache für Kinder von 9 bis 13 Jahren, the initial section of which delved into the structure and logic of language, potentially influencing young Frege's future interests.

After his father's death, Frege's mother, Auguste Wilhelmine Sophie Frege (née Bialloblotzky, 1815-1898), took over the leadership of the school. Auguste was a descendant of Philipp Melanchthon, and her father, Johann Heinrich Siegfried Bialloblotzky, hailed from a Polish noble family that had migrated from Poland in the 17th century. Frege was raised as a Lutheran.

Frege received his early education at the Gymnasium in Wismar, known as the Große Stadtschule Wismar, graduating in 1869. His mathematics and natural science teacher, Gustav Adolf Leo Sachse (1843-1909), who was also a poet, recognized Frege's mathematical talent and encouraged him to pursue higher education at his own alma mater, the University of Jena.

In the spring of 1869, Frege matriculated at the University of Jena as a citizen of the North German Confederation. Over four semesters, he attended approximately twenty lecture courses, primarily focusing on mathematics and physics. His most influential teacher at Jena was Ernst Karl Abbe (1840-1905), a physicist, mathematician, and inventor. Abbe lectured on topics such as the theory of gravity, galvanism, electrodynamics, complex analysis, applications of physics, and mechanics. Beyond being a teacher, Abbe became a trusted friend and, as director of the optical manufacturer Carl Zeiss AG, was in a position to support Frege's academic career. Their correspondence grew closer after Frege's graduation. Other notable teachers at Jena included Christian Philipp Karl Snell (mathematics and physics), Hermann Schaeffer (mathematics and applied physics), and the philosopher Kuno Fischer (Kantian and critical philosophy).

In 1871, Frege transferred to the University of Göttingen, which was then the leading university for mathematics in German-speaking territories. There, he attended lectures by prominent scholars such as Alfred Clebsch (analytic geometry), Ernst Christian Julius Schering (function theory), Wilhelm Eduard Weber (physical studies, applied physics), Eduard Riecke (theory of electricity), and Hermann Lotze (philosophy of religion). Many philosophical doctrines developed by the mature Frege show parallels with Lotze's ideas, leading to scholarly debate about a direct influence.

Frege completed his doctorate in 1873 under Ernst Christian Julius Schering. His dissertation, "Ueber eine geometrische Darstellung der imaginären Gebilde in der Ebene" ("On a Geometrical Representation of Imaginary Forms in a Plane"), aimed to address fundamental problems in geometry, such as the mathematical interpretation of infinitely distant (imaginary) points in projective geometry.

2.2. Academic Career and Marriage

After earning his doctorate, Frege completed his Habilitation at the University of Jena in 1874, qualifying him to teach at a university level. He then began his academic career as a Privatdozent (private lecturer) in mathematics at Jena. In 1879, he was appointed Ausserordentlicher Professor (associate professor) at the University of Jena. His career progressed, and in 1896, he was promoted to Ordentlicher Honorarprofessor (full honorary professor) at the same institution. He retired from the University of Jena in 1918.

On March 14, 1887, Frege married Margarete Katharina Sophia Anna Lieseberg (1856-1904). The couple faced personal tragedy, as at least two of their children died in infancy. Years later, they adopted a son named Alfred. Beyond these details, little is known about Frege's private family life.

3.1. Begriffsschrift and the Foundations of Modern Logic

Frege's seminal 1879 work, Begriffsschrift (Concept Script: A Formal Language for Pure Thought Modeled on that of Arithmetic), represented a profound departure from traditional logic, which had remained largely unchanged since Aristotle. This publication ushered in a new era of logical inquiry.

In Begriffsschrift, Frege introduced predicate logic, a system that extended the capabilities of propositional logic by allowing for the analysis of the internal structure of propositions. A key innovation was the rigorous treatment of mathematical functions and variables, leading to the invention of quantified variables. This allowed for the precise expression of logical statements involving "some" and "all" and effectively solved the problem of multiple generality, which traditional logic struggled to represent. For example, while Aristotelian logic could not adequately represent mathematical statements like Euclid's theorem (that there are an infinite number of prime numbers), Frege's "conceptual notation" could.

Frege's notation in Begriffsschrift was unique and had no direct antecedents, nor has it been widely imitated since. However, the underlying concepts he introduced, such as the axiomatic approach to logic and the use of quantified variables, became ubiquitous in mathematics and logic.

His notation for logical concepts included:

Concept	Begriffsschrift Notation	Modern Notation
Negation		¬A
Implication		B → A
Universal Quantifier		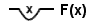∀x: F(x)
Existential Quantifier		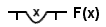∃x: F(x)
Equivalence	A ≡ B	A ↔ B

3.2. Logicism and The Foundations of Arithmetic

A central aim of Frege's work was to establish logicism, the philosophical view that mathematics, particularly arithmetic, is reducible to logic and can be derived entirely from logical principles without recourse to intuition or non-logical axioms. He sought to demonstrate that arithmetic is a branch of logic, distinct from geometry, which might rely on intuition.

This idea was articulated in non-symbolic terms in his 1884 work, The Foundations of Arithmetic (Die Grundlagen der Arithmetik). In this book, Frege launched a strong critique of psychologism, the view that logical and mathematical concepts are rooted in mental processes or psychological states. He argued against psychologistic definitions of number, asserting that the concept of number is not a synthetic (empirical) concept but an analytic (logical) one. His purpose was not to answer general questions about meaning but to explore the foundations of arithmetic, addressing questions like "What is a number?" and "What objects do number-words refer to?"

3.3. Grundgesetze der Arithmetik and the Logicist Program

Frege's most ambitious attempt to realize his logicist program was in Grundgesetze der Arithmetik (Basic Laws of Arithmetic), published in two volumes (Vol. 1 in 1893, Vol. 2 in 1903, the latter at his own expense). In this work, he aimed to formally derive all the laws of arithmetic from logical axioms using his symbolic system. Most of these axioms were carried over from Begriffsschrift, with some significant modifications.

The crucial new principle introduced in Grundgesetze was what Frege called Basic Law V. In modern notation, this law states that the "value-range" (or extension) of a function f(x) is the same as the "value-range" of a function g(x) if and only if for all x, f(x) equals g(x). More specifically, for predicates Fx and Gx, Basic Law V states that their extensions ({x|Fx} and {x|Gx}) are the same if and only if for all x, Fx is logically equivalent to Gx.

A famous episode occurred in 1903, just as Vol. 2 of Grundgesetze was about to be published. Bertrand Russell wrote to Frege, demonstrating that Russell's paradox could be derived from Basic Law V. Russell pointed to "the set of things x that are such that x is not a member of x." Frege's system, based on Basic Law V, implied that this set both is and is not a member of itself, rendering the system inconsistent. Frege, with exceptional honesty, added a hasty, last-minute Appendix to Vol. 2, acknowledging the contradiction and proposing a modification to Basic Law V to eliminate it. He wrote: "Hardly anything more unfortunate can befall a scientific writer than to have one of the foundations of his edifice shaken after the work is finished."

Frege's proposed remedy was later shown by Stanisław Leśniewski in 1938 to be flawed, implying that there could be only one object in the universe of discourse, which would contradict other fundamental assumptions in his system. However, recent work by philosophers and mathematical logicians has shown that much of the logicist program of Grundgesetze might be salvaged through other modifications:

• Weakened Basic Law V:** George Boolos proposed weakening Basic Law V to V*, which is consistent if second-order arithmetic is, and suffices to prove the axioms of second-order arithmetic.
• Hume's Principle:** Basic Law V can be replaced with Hume's principle, which states that the number of Fs is the same as the number of Gs if and only if the Fs can be put into a one-to-one correspondence with the Gs. This principle, too, is consistent if second-order arithmetic is, and suffices to prove its axioms. This result is known as Frege's theorem because Frege's derivation of arithmetic principles primarily relied on Hume's principle, which he derived from Basic Law V.
• Predicative Second-Order Logic:** Frege's logic, now known as second-order logic, can be weakened to so-called predicative second-order logic. When combined with Basic Law V, this system is provably consistent by finitistic or constructive methods, though it can only interpret very weak fragments of arithmetic.

3.4. Impact on Mathematical Logic

Frege's innovations in logic, including his formal systems and concepts, profoundly influenced subsequent developments in mathematical logic. His work provided the analytical tools and formal machinery that were essential to later foundational works.

His ideas were crucial for Bertrand Russell and Alfred North Whitehead's monumental Principia Mathematica (3 vols., 1910-1913), which aimed to derive all of mathematics from a set of logical axioms. Russell's theory of descriptions also drew heavily on Frege's analysis of logical concepts. Furthermore, Frege's formal systems were foundational for Kurt Gödel's (1906-1978) incompleteness theorems and Alfred Tarski's (1901-1983) theory of truth.

Despite the initial lack of international attention, Frege's logical ideas began to spread, particularly after Russell's 1903 appendix to The Principles of Mathematics highlighted his differences with Frege. His work was further disseminated through the writings of his student Rudolf Carnap (1891-1970) and other admirers, including Russell and Ludwig Wittgenstein (1889-1951). Frege is widely considered the greatest logician since Aristotle, and one of the most profound philosophers of mathematics in history.

4.1. Sense and Reference (Sinn und Bedeutung)

In his highly influential 1892 paper, "On Sense and Reference" ("Über Sinn und Bedeutung"), Frege introduced a crucial distinction between the 'sense' (Sinn) and 'reference' (Bedeutung) of an expression. While traditional accounts of meaning often considered expressions to have only one feature (their reference), Frege argued that expressions possess two distinct aspects of significance.

The reference (or Bedeutung, also translated as "meaning" or "denotation") of a proper name, such as "Tom," is simply the entity to which it refers (the person named Tom). Frege extended this concept to propositions, asserting that a complete sentence "refers" to its truth-value (either the True or the False).

By contrast, the sense (or Sinn) of an expression is its "mode of presentation" or the way in which its object is given. For a complete sentence, its sense is the thought it expresses. A key insight of this distinction is that multiple expressions can have the same reference but different senses. For example, "the morning star" and "the evening star" both refer to the planet Venus, but they present Venus in different ways, thus having different senses. Similarly, the name "Charles Philip Arthur George Mountbatten-Windsor" and the functional expression "the King of the United Kingdom" have the same referent, King Charles III, but convey different senses.

This distinction has been a subject of ongoing debate, notably disputed by Bertrand Russell in his paper "On Denoting" and further explored by Saul Kripke in his lectures "Naming and Necessity".

4.2. Concept and Object (Begriff und Gegenstand)

Frege's 1892 paper, "Concept and Object" ("Ueber Begriff und Gegenstand"), detailed his analysis of the distinction between logical concepts and objects. For Frege, concepts are functions that map objects to truth-values, while objects are complete and saturated entities. This distinction is fundamental to his understanding of predication and the structure of thought, asserting that concepts are intrinsically "unsaturated" and require an object to be completed.

4.3. Other Key Linguistic Concepts

Frege's philosophy of language also introduced several other important concepts:

• Function and Argument Analysis of the Proposition:** Frege viewed propositions as composed of functions and arguments, similar to mathematical expressions. This allowed for a more detailed logical analysis of sentence structure than previously possible.
• Principle of Compositionality:** This principle states that the meaning of a complex expression is determined by the meanings of its constituent expressions and the way they are combined. This idea is foundational to modern semantics.
• Context Principle:** Articulated in The Foundations of Arithmetic, this principle states that a word has meaning only in the context of a sentence. It emphasizes that words do not have independent meanings in isolation but acquire their meaning through their role in a complete thought or proposition.

5.1. Critique of Psychologism

Frege was a staunch opponent of psychologism, the philosophical position that logical and mathematical laws are derived from or dependent on human psychological processes or mental states. He argued vigorously that logical laws are objective and universal, existing independently of any individual's mind or cognitive faculties. For Frege, the truth of a logical proposition is not contingent on how humans think or perceive it. He believed that psychologism blurred the distinction between the objective validity of a thought and the subjective act of thinking, thereby undermining the objectivity and certainty of logic and mathematics. This critique was central to his defense of logicism, as he sought to establish arithmetic on a purely logical, non-psychological foundation.

5.2. Platonism

Frege held a realist or Platonist view regarding numbers, propositions, and other abstract entities. He asserted that these entities exist independently of the human mind and are not created by thought. For Frege, numbers are objective, mind-independent objects, and propositions (or "thoughts," as he called them) are abstract, timeless entities that exist in a "third realm," distinct from both the physical world and individual mental states. This Platonist stance provided the metaphysical underpinning for his anti-psychologism, ensuring the objectivity and universality of logical and mathematical truths.

6.1. Political Views and the 1924 Diary

In the last year of his life, at the age of 76, Frege kept a private diary in 1924 that contained stark political opinions. These views were deeply conservative, anti-parliamentary, anti-democratic, and anti-liberal. He expressed strong negative sentiments towards Catholics, the French, and particularly Jews, whom he believed should be deprived of political rights and, ideally, expelled from Germany. Frege confided that he had once considered himself a liberal and an admirer of Otto von Bismarck, but after the German Revolution of 1918-1919, his political opinions became more radical, leading him to sympathize with General Erich Ludendorff. In an entry dated May 5, 1924, Frege explicitly expressed agreement with an article published in Houston Stewart Chamberlain's Deutschlands Erneuerung that praised Adolf Hitler. He recorded the belief that it would be best if the Jews of Germany would "get lost, or better would like to disappear from Germany." The diary also contained a critique of universal suffrage and socialism.

The revelation of these views, particularly his antisemitism, came as a shock to many scholars, including Frege expert Michael Dummett, who described his dismay upon discovering his hero's prejudices. This aspect of Frege's personal life presents a complex challenge to his philosophical legacy. It is noteworthy that, despite these private sentiments, Frege maintained friendly relations with Jewish individuals in his real life. For instance, Gershom Scholem, a Jewish student, greatly valued Frege's teaching, and it was Frege who encouraged Ludwig Wittgenstein to go to England to study with Bertrand Russell. The 1924 diary was published posthumously in 1994.

8.1. Early Neglect and Later Rediscovery

During his lifetime, Frege's groundbreaking work was largely overlooked by the broader philosophical and mathematical communities. His unique diagrammatic notation, which he developed for his logical system, had no historical antecedents and found no imitators, contributing to the difficulty of its reception. Furthermore, until the publication of Russell and Whitehead's Principia Mathematica in 1910-1913, the dominant approach to mathematical logic remained that of George Boole and his intellectual descendants, such as Ernst Schröder. Consequently, Frege's profound contributions did not receive the recognition they deserved while he was alive.

However, in the mid-20th century, there was a significant rediscovery and re-evaluation of Frege's work. This renewed attention, greatly facilitated by the efforts of figures like Bertrand Russell and Ludwig Wittgenstein, led to his ideas becoming foundational for analytic philosophy.

8.2. Influence on Analytic Philosophy and Key Thinkers

Frege's ideas profoundly impacted major figures in 20th-century philosophy, shaping the trajectory of analytic philosophy.

• Ludwig Wittgenstein**: Wittgenstein's early work, particularly the Tractatus Logico-Philosophicus, was heavily influenced by Frege's logic and philosophy of language, especially his ideas on the nature of propositions and the relationship between language and reality.
• Bertrand Russell**: Although Russell's discovery of the paradox in Frege's system was a major setback for Frege's logicist program, Russell himself was deeply influenced by Frege's logical innovations. His own work, including The Principles of Mathematics and Principia Mathematica, built upon and adapted many of Frege's formal techniques.
• Rudolf Carnap**: As Frege's student, Carnap was instrumental in disseminating Frege's logical ideas, particularly within the Vienna Circle and the broader movement of logical positivism.
• Edmund Husserl**: Husserl, the founder of phenomenology, initially held views closer to psychologism but was persuaded by Frege's critique to adopt a more objective stance on logical truths.

Frege's distinctions between sense and reference, concept and object, and his critique of psychologism became central tenets and starting points for subsequent discussions in the philosophy of language, metaphysics, and epistemology within the analytic tradition.

8.3. Modern Re-evaluations of Logicism

Despite the setback caused by Russell's Paradox, there have been significant modern efforts to reconstruct or defend Frege's logicist program. Logicians and philosophers such as Charles Parsons, George Boolos, and Richard Heck have explored ways to modify or reinterpret Frege's system to avoid the paradox while retaining its core insights. The discovery of Frege's theorem, which shows that the axioms of second-order arithmetic can be derived from Hume's principle (a principle that Frege himself used in his derivations and that is weaker than Basic Law V), has led to a renewed interest in the viability of a neo-Fregean logicism. These re-evaluations highlight the enduring power and depth of Frege's original ideas, demonstrating that much of his foundational work can be preserved and built upon even in light of the paradox.