1. Overview
Johann Carl Friedrich Gauss, a German polymath born in 1777, is celebrated as one of the most influential mathematicians and scientists in history. His genius, evident from a very young age, propelled him to make groundbreaking contributions across diverse fields including number theory, algebra, analysis, differential geometry, astronomy, geodesy, and physics. Gauss's rigorous methods and prolific discoveries, many of which remained unpublished during his lifetime, profoundly shaped the development of modern mathematics and laid critical foundations for various scientific disciplines. His work on orbital mechanics, geomagnetism, and error theory had immediate practical applications, while his theoretical insights into non-Euclidean geometry and complex analysis anticipated future mathematical revolutions. Gauss's enduring legacy is reflected in the numerous concepts, theorems, and units named after him, solidifying his status as a titan of science whose impact continues to resonate in scientific and technological advancements worldwide.
2. Biography
Carl Friedrich Gauss's life was a journey marked by extraordinary intellectual prowess, personal challenges, and an unwavering dedication to scientific discovery, which led him from humble beginnings to a position of immense influence in the academic world.
2.1. Youth and education


Gauss was born on 30 April 1777 in Brunswick, in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany). His family was of relatively low social status; his father, Gebhard Dietrich Gauss (1744-1808), worked variously as a butcher, bricklayer, gardener, and treasurer of a death-benefit fund. Gauss described his father as honorable and respected, but also rough and dominating at home. His mother, Dorothea, Carl Friedrich's second wife, was nearly illiterate, though his uncle and mother were supportive of his academic pursuits. Gauss had an elder brother from his father's first marriage.
Gauss was a remarkable child prodigy in mathematics. A popular anecdote recounts that at the age of seven, his elementary school teacher, J.G. Büttner, assigned the task of summing all integers from 1 to 100. Young Gauss quickly produced the correct answer, 5050, by recognizing that he could pair the numbers (1+100, 2+99, etc.) to get 50 pairs each summing to 101, thus 50 × 101 = 5050. This story, while possibly embellished, illustrates his early grasp of arithmetic progressions. Another anecdote suggests that at age three, he corrected his father's payroll calculations.
Recognizing his extraordinary abilities, his teachers brought him to the attention of Charles William Ferdinand, Duke of Brunswick, who provided him with a scholarship. Gauss attended the local Collegium Carolinum (a precursor to the Technical University of Braunschweig, though not yet a full university at his time) from 1792 to 1795, where Eberhard August Wilhelm von Zimmermann was one of his teachers. The Duke then funded his studies in mathematics, sciences, and classical languages at the University of Göttingen from 1795 to 1798. His mathematics professor was Abraham Gotthelf Kästner, whom Gauss humorously called "the leading mathematician among poets, and the leading poet among mathematicians." He held his physics teacher, Georg Christoph Lichtenberg, and classics teacher, Christian Gottlob Heyne, in high regard. His fellow students included Johann Friedrich Benzenberg, Farkas Bolyai, and Heinrich Wilhelm Brandes.
Gauss was largely self-taught in mathematics, independently rediscovering several theorems. A pivotal moment occurred in 1796 when he solved a geometrical problem that had puzzled mathematicians since Ancient Greece: he determined which regular polygons can be constructed using only a compass and straightedge. This discovery, particularly the constructibility of the regular heptadecagon (17-sided polygon), led him to choose mathematics over philology as his career. He was so proud of this achievement that he reportedly requested a regular 17-gon be engraved on his tombstone, though a star with 17 points was eventually used due to practical difficulties. Gauss's mathematical diary, a collection of brief notes on his results from 1796 to 1814, reveals that many ideas for his magnum opus, Disquisitiones Arithmeticae (1801), originated during this period.
2.2. Private scholar
Gauss earned his Doctor of Philosophy degree in absentia in 1799 from the University of Helmstedt, at the special request of the Duke of Brunswick, with Johann Friedrich Pfaff assessing his doctoral thesis. The Duke continued to support him financially as a private scholar in Brunswick. During this period, Gauss declined offers from the Russian Academy of Sciences in St. Petersburg and Landshut University. The Duke also promised to fund the establishment of an observatory in Brunswick in 1804, with preliminary designs by architect Peter Joseph Krahe. However, these plans were thwarted by the War of the Fourth Coalition: the Duke was killed in the Battle of Jena-Auerstedt in 1806, leading to the abolition of the duchy and the cessation of Gauss's financial support.
In the early 19th century, while calculating asteroid orbits, Gauss connected with the astronomical community in Bremen and Lilienthal, particularly Wilhelm Olbers, Karl Ludwig Harding, and Friedrich Wilhelm Bessel. They were part of the informal group of astronomers known as the Celestial police, whose goal included discovering new planets. They collected data on asteroids and comets, which served as the basis for Gauss's research on orbital mechanics, later published in his astronomical masterpiece Theoria motus corporum coelestium (1809).
2.3. Professor in Göttingen

In November 1807, Gauss accepted a position as a full professor and director of the Göttingen Observatory at the University of Göttingen, then part of the newly established Kingdom of Westphalia under Jérôme Bonaparte. He held this chair until his death in 1855. Upon his appointment, he faced a demand for 2.00 K FRF as a war contribution, which he could not afford. Although Wilhelm Olbers and Pierre-Simon Laplace offered to help, Gauss refused their assistance. The sum was eventually paid anonymously by Prince-primate Karl Theodor Anton Maria von Dalberg.
The observatory, founded in 1748, was 60 years old and housed usable but partly outdated instruments. The construction of a new observatory had been approved in principle since 1802 by George III, and the Westphalian government continued the planning. Gauss moved into the new facility in September 1816, which was equipped with modern instruments, including two meridian circles from Johann Georg Repsold and Georg Friedrich von Reichenbach, and a heliometer from Joseph von Fraunhofer.
Gauss's scientific activities, beyond pure mathematics, shifted focus over his career: astronomy dominated the first two decades of the 19th century, geodesy the third, and physics, particularly magnetism, the fourth.
Despite his continuous lecturing from 1808 until 1854, Gauss openly expressed his aversion to teaching, viewing it as a burden and a waste of his time. He primarily lectured on astronomy (70%), with smaller percentages on mathematical (15%), geodetical (9%), and physical (6%) subjects, and only three lectures dedicated to pure mathematics. Nevertheless, some of his students became highly influential mathematicians, physicists, and astronomers, including Moritz Cantor, Richard Dedekind, Johann Franz Encke, August Ferdinand Möbius, and Bernhard Riemann.
Gauss did not write textbooks and disliked the popularization of scientific matters. His only attempts at popularization were his works on the date of Easter (1800/1802) and the essay Erdmagnetismus und Magnetometer (1836). He published his papers and books exclusively in Latin or German; for instance, his Theoria motus... was originally completed in German in 1806 but translated into Latin at the editor's request. He wrote Latin in a classical style with some contemporary mathematical modifications.

In his inaugural lecture at Göttingen University in 1808, Gauss emphasized that reliable observations and results obtained through rigorous calculation were the sole tasks of astronomy. He was supported by colleagues who complemented the educational program, such as mathematician Thibaut and physicist Johann Tobias Mayer. After 1831, Wilhelm Eduard Weber joined as his successor in physics, and Karl Ludwig Harding handled most practical astronomy lectures at the observatory. Gauss lived in the western wing of the new observatory, and Harding in the eastern. Though initially friendly, their relationship soured, possibly because Gauss saw Harding more as an assistant than an equal, even attempting to find him a position outside Göttingen. Gauss largely monopolized the new meridian circles, rarely sharing them with Harding.
Despite the new, well-equipped observatory, Gauss's astronomical research became a "one-man enterprise" without a long-term observation program. The university only appointed an assistant after Harding's death in 1834, with Carl Wolfgang Benjamin Goldschmidt and later Wilhelm Klinkerfues serving in the role. Gauss twice declined offers from Berlin (1810, 1825) to become a full member of the Prussian Academy without lecturing duties, and also from Leipzig University (1810) and Vienna University (1842), possibly due to his difficult family situation. His salary increased significantly over the years, making him one of the university's best-paid professors.
Gauss supported his colleagues, providing an honorary degree for Friedrich Wilhelm Bessel from Göttingen's Philosophy Faculty in 1811 and recommending an honorary degree for Sophie Germain shortly before her death (though she never received it). He also successfully supported mathematician Gotthold Eisenstein in Berlin.
Gauss remained loyal to the House of Hanover. When King William IV died in 1837, the new Hanoverian King Ernest Augustus annulled the 1833 constitution. Seven professors, known as the "Göttingen Seven"-including his friend and collaborator Wilhelm Weber and his son-in-law Heinrich Ewald-protested and were dismissed. Three were expelled, though Ewald and Weber remained in Göttingen. Gauss was deeply affected but could not help them.
Gauss participated in academic administration, serving three times as dean of the Faculty of Philosophy. He managed the university's widow's pension fund, applying actuarial science to stabilize benefits. He was also appointed director of the Royal Academy of Sciences in Göttingen for nine years.
2.4. Family
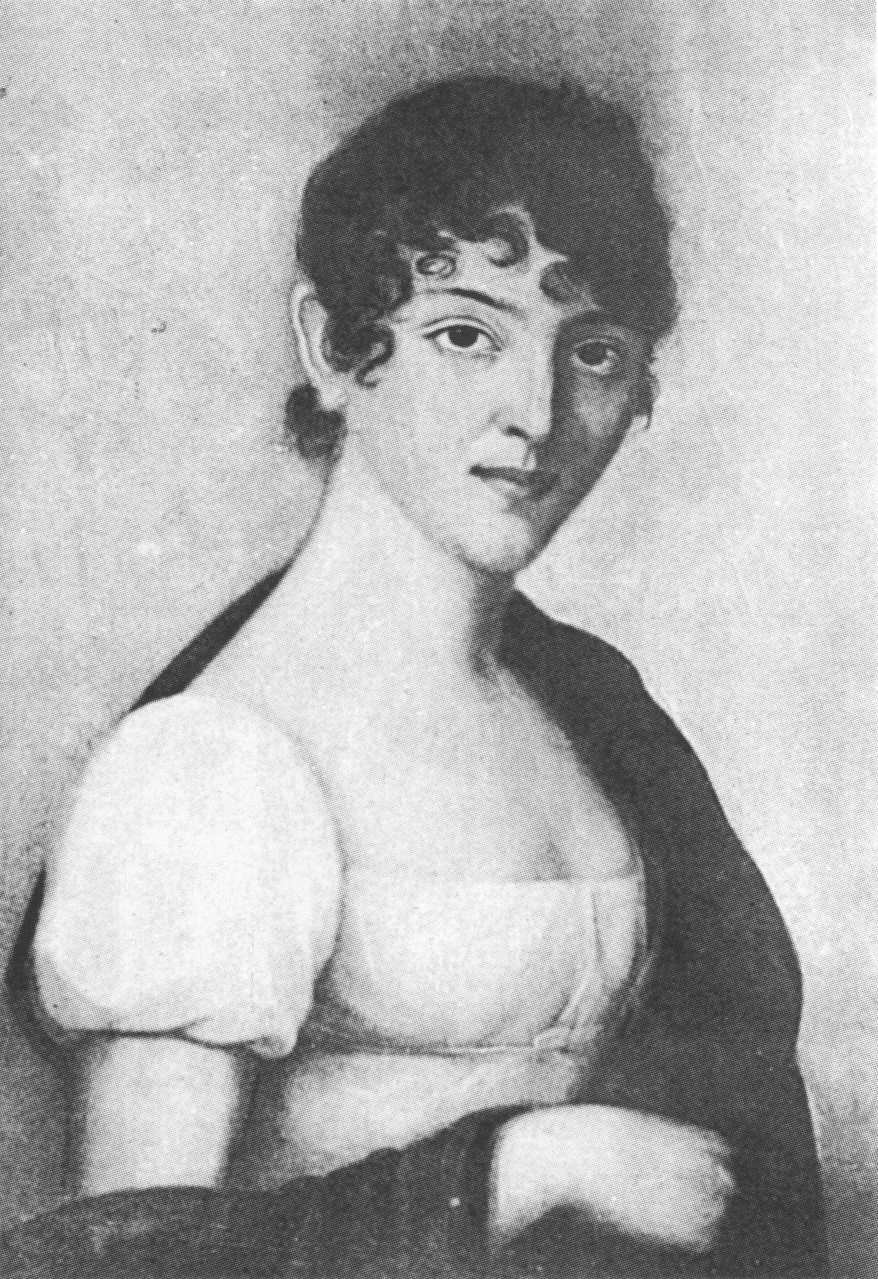
Gauss's personal life was marked by significant joy and profound sorrow. On 9 October 1805, he married Johanna Osthoff in St. Catherine's church in Brunswick. They had three children: Joseph (1806-1873), Wilhelmina (1808-1840), and Louis (1809-1810). Johanna's sudden death on 11 October 1809, one month after Louis's birth, and Louis's death a few months later, deeply affected Gauss. He expressed his grief in a poignant letter to his deceased wife, one of his most personal surviving documents. He named his children in honor of the discoverers of the first asteroids: Giuseppe Piazzi, Wilhelm Olbers, and Karl Ludwig Harding.
On 4 August 1810, Gauss married Wilhelmine (Minna) Waldeck, a friend of his first wife. They had three more children: Eugen (later Eugene) (1811-1896), Wilhelm (later William) (1813-1879), and Therese (1816-1864). Minna Gauss suffered from a serious illness for over a decade and died on 12 September 1831. His daughters, Wilhelmina and Therese, later also suffered from the same disease. After Minna's death, Therese took over the household and cared for Gauss for the remainder of his life. She later married actor Constantin Staufenau. His eldest daughter, Wilhelmina, married the orientalist Heinrich Ewald. Gauss's mother, Dorothea, lived with him from 1817 until her death in 1839.
Gauss's relationships with his sons were complex. His eldest son, Joseph, assisted his father during a survey campaign in 1821 while still a schoolboy. After a brief university stint, Joseph joined the Hanoverian army in 1824 and continued to assist in surveying. In the 1830s, he expanded the survey network to the western parts of the kingdom. With his geodetic qualifications, he left military service to become director of the Royal Hanoverian State Railways, studying railroad systems in the US for several months in 1836, where he met geodesist Ferdinand Rudolph Hassler, a correspondent of Carl Friedrich Gauss. Joseph often required financial support from his father even after marriage.
Eugen, the second son, possessed a talent for computation and languages but had a vivacious and rebellious character. Gauss wanted him to become a lawyer, but Eugen preferred philology. After incurring debts and causing a public scandal, Eugen dramatically left Göttingen in September 1830 and emigrated to the United States. He initially squandered his money, leading his father to refuse further financial support. Eugen worked for the American Fur Company in the Midwest and later became a successful businessman in Missouri.
The youngest son, Wilhelm, struggled to get an appropriate education for agricultural administration and also emigrated to the United States. He settled in Missouri, starting as a farmer and later becoming wealthy in the shoe business in St. Louis. Both Eugen and Wilhelm have numerous descendants in America. In Germany, Gauss's descendants all trace back to Joseph, as his daughters had no children.
Gauss's family life was often overshadowed by these difficulties. He once described himself as "the victim of the worst domestic sufferings" in a letter to Bessel in December 1831.
2.5. Personality and beliefs
Gauss's personality was a blend of intense scholarly rigor, a reserved demeanor, and deeply held personal convictions.
2.5.1. Scholar


In the early 19th century, Gauss stood as the foremost mathematician in Germany, comparable to the leading French mathematicians of his time. His Disquisitiones Arithmeticae was the first German mathematical book to be translated into French.
Gauss was at the forefront of new mathematical developments, characterized by a wealth of original ideas and an unprecedented rigor in his proofs. Unlike earlier mathematicians such as Leonhard Euler, who often shared their thought processes, including errors, Gauss introduced a new style of direct and complete explanation that did not reveal the author's path to discovery. This commitment to rigor was encapsulated in his personal motto, Pauca sed MaturaFew, but RipeLatin, which he inscribed on his personal seal. He refused to publish work he did not consider perfectly complete and beyond criticism. Many colleagues urged him to publish more, but Gauss defended his approach, stating that while initial discoveries were easy, preparing a presentable elaboration required significant time and "serenity of mind." Despite this, he published many short communications on urgent topics and left a considerable literary estate.
For himself, Gauss held a different ideal: "It is not knowledge, but the act of learning, not possession but the act of getting there, which grants the greatest enjoyment. When I have clarified and exhausted a subject, then I turn away from it, in order to go into darkness again."
His posthumously published papers, scientific diary, and personal notes reveal that he worked extensively through empirical methods. He was a lifelong, enthusiastic calculator, performing calculations with extraordinary speed and often without precise initial control, instead relying on masterful estimation to check results. While not always error-free, he managed his enormous workload with skillful tools, including extensive use and construction of mathematical tables, and development of methods like Gaussian elimination. He often performed calculations with much higher precision than required, preparing tables with more decimal places than practical purposes demanded, which likely aided his discovery of theorems in number theory.
Gauss referred to mathematics as "the queen of sciences" and arithmetic as "the queen of mathematics." He supposedly believed that understanding Euler's identity was a benchmark for becoming a first-class mathematician. Gauss's concept of priority differed from his contemporaries; he believed priority belonged to "the first to discover, not the first to publish." He was sometimes criticized for his negligent way of quoting, defending himself by saying that proper, complete referencing required historical knowledge and time he preferred to spend on research.
2.5.2. Private man

Soon after Gauss's death, his friend Sartorius published the first biography (1856), portraying him as a serene, forward-striving man with childlike modesty, but also possessing an "iron character" and unshakeable strength of mind. Outside his close circle, he was perceived as reserved and unapproachable, like an "Olympian sitting enthroned on the summit of science." Contemporaries generally agreed that Gauss had a difficult character; he often refused compliments and could be grumpy, though his mood could quickly shift to a charming, open-minded host. He detested polemic natures, opposing Justus Liebig's appointment to a Göttingen chair due to Liebig's involvement in controversies.
Gauss's life was significantly affected by severe family problems. The sudden death of his first wife, Johanna, after the birth of their third child, caused him immense grief, as evidenced by his deeply personal letter to her. The situation worsened with his second wife, Minna, who suffered from tuberculosis for over a decade, a disease that later afflicted both his daughters. Gauss rarely expressed his distress openly, though he once described himself as "the victim of the worst domestic sufferings" in a letter to Bessel.
His younger sons were educated away from Göttingen due to their mother's illness. His eldest son, Joseph, despite acquiring considerable geodetic knowledge, ended his military career as a poorly paid first lieutenant and often needed financial support from his father. Eugen, the second son, shared his father's talent for computation and languages but had a vivacious and rebellious character. Their differing career aspirations and Eugen's debts led to a dramatic departure to the United States, after which Gauss refused further financial aid. Wilhelm, the youngest son, also struggled with education and emigrated. Only his youngest daughter, Therese, remained with him in his final years.
In his later years, Gauss developed a habit of collecting numerical data on various subjects, both useful and trivial, such as the number of paths from his home to certain places in Göttingen or the lifespans of individuals. He famously congratulated Alexander von Humboldt in December 1851 for reaching the same age as Isaac Newton, calculated in days.
Gauss was proficient in modern languages, in addition to his excellent knowledge of Latin. At 62, he began to teach himself Russian, likely to read scientific works from Russia, including those of Nikolai Lobachevsky on non-Euclidean geometry. He read classical and modern literature, including English and French works in their original languages. His favorite English author was Walter Scott, and his favorite German author was Jean Paul. He enjoyed singing and attending concerts and was an avid newspaper reader, often visiting the university's academic press salon. Gauss had little regard for philosophy, mocking the "splitting hairs of the so-called metaphysicians," referring to proponents of Naturphilosophie.
Gauss possessed an "aristocratic and thoroughly conservative nature," with little respect for people's intelligence and morals, adhering to the motto "mundus vult decipi" (the world wants to be deceived, so let it be deceived). He disliked Napoleon and his system, and all forms of violence and revolution filled him with horror. He condemned the methods of the Revolutions of 1848, though he agreed with some of their aims, such as the idea of a unified Germany. He held a low opinion of the constitutional system, criticizing contemporary parliamentarians for their lack of knowledge and logical errors.
Speculation surrounds Gauss's religious beliefs. He sometimes stated, "God arithmetizes" and "I succeeded - not on account of my hard efforts, but by the grace of the Lord." As a member of the Lutheran church, like most in northern Germany, he did not appear to interpret all dogmas literally. Sartorius noted Gauss's religious tolerance and believed his "insatiable thirst for truth" and sense of justice were religiously motivated. He believed that science revealed the immortal core of the human soul and that a life well-lived on Earth was the best preparation for heaven. He saw God's revelation as continuous, not confined to sacred texts, and believed a book was inspired if it inspired him. He firmly believed in personal immortality, a final adjustment of things, and an eternal, just, omniscient God with infinite power, which formed the bedrock of his religious life, intertwined with his scientific pursuits.
2.6. Death and legacy

Gauss remained mentally active into his old age, despite suffering from gout and general unhappiness. He died of a heart attack on 23 February 1855 in Göttingen, at the age of 77. He was interred in the Albani Cemetery there. Heinrich Ewald, his son-in-law, and Wolfgang Sartorius von Waltershausen, his close friend and biographer, delivered eulogies at his funeral.
Gauss was a successful investor, accumulating considerable wealth through stocks and securities, totaling over 150.00 K GRD (Thaler). After his death, approximately 18.00 K GRD were discovered hidden in his rooms.
The day after Gauss's death, his brain was removed, preserved, and studied by Rudolf Wagner, who found its mass to be slightly above average, at 0.1 K oz (1.49 K g). Wagner's son, Hermann, a geographer, estimated the cerebral area to be 219.59 K mm2 in his doctoral thesis. However, in 2013, a neurobiologist at the Max Planck Institute for Biophysical Chemistry in Göttingen discovered that Gauss's brain had been mistakenly swapped with that of physician Conrad Heinrich Fuchs, who died a few months after Gauss, due to mislabeling. Thus, all investigations on Gauss's brain until 1998, except the initial ones by Rudolf and Hermann Wagner, actually referred to Fuchs's brain. Subsequent investigations found no remarkable anomalies in either brain.
Gauss's meticulousness and reluctance to publish incomplete work led to many of his discoveries remaining in his private notes for years or decades. This perfectionism, while ensuring the highest quality of his published works, also meant that he did not receive immediate credit for many breakthroughs. The mathematical historian Eric Temple Bell famously stated that if Gauss had published all his discoveries in a timely manner, mathematics would have advanced by 50 years.
Despite his dislike for teaching, some of his students, including Richard Dedekind and Bernhard Riemann, became highly influential mathematicians, carrying forward and expanding upon his ideas. Gauss is widely considered one of the greatest mathematicians of all time, often referred to as the "Prince of Mathematicians," a title that reflects his profound and lasting impact on the field.
3. Scientific work
Gauss's scientific work spanned an astonishing range of disciplines, from pure mathematics to astronomy and physics, where he consistently introduced revolutionary concepts and rigorous methods.
3.1. Mathematics
Gauss's contributions to mathematics were foundational, transforming numerous fields and setting new standards for rigor and depth.
3.1.1. Number theory
Gauss's foundational contributions to number theory are largely encapsulated in his masterpiece, Disquisitiones Arithmeticae, published in 1801. He began working on number theory in 1795, realizing that many of his independent discoveries had already been found by predecessors like Fermat, Euler, Lagrange, and Legendre.
In Disquisitiones Arithmeticae, Gauss consolidated number theory as a distinct discipline, covering both elementary and algebraic aspects. He introduced the triple bar symbol (≡) for congruence and used it to present modular arithmetic clearly. The work addresses the unique factorization theorem and primitive roots modulo n. It also presents the first two proofs of the law of quadratic reciprocity and develops the theories of binary and ternary quadratic forms. The book includes the Gauss composition law for binary quadratic forms and the enumeration of the number of representations of an integer as the sum of three squares. As a direct corollary of his theorem on three squares, he proved the triangular case of the Fermat polygonal number theorem for n = 3. From analytic results on class numbers given without proof, it appears Gauss knew the class number formula by 1801.
In the final section, Gauss provided a proof for the constructibility of a regular heptadecagon (17-sided polygon) with straightedge and compass, by reducing this geometrical problem to an algebraic one. He showed that a regular polygon is constructible if its number of sides is a power of 2 or the product of a power of 2 and any number of distinct Fermat primes. This section also gives a result on the number of solutions of certain cubic polynomials with coefficients in finite fields, which relates to counting integral points on an elliptic curve. An unfinished eighth chapter, containing work from 1797-1799, was discovered posthumously.
One of Gauss's earliest results was the empirically conjectured prime number theorem in 1792, which estimates the number of prime numbers using the integral logarithm.
When encouraged in 1816 to compete for a French Academy prize on Fermat's Last Theorem (FLT), Gauss declined due to his low esteem for the problem. However, among his papers, a short undated manuscript was found with proofs of FLT for the cases n = 3 and n = 5. While Euler had proved n = 3 earlier, Gauss's proof was more streamlined, using Eisenstein integers and offering a simpler approach than in the real integers case.
In 1831, Gauss contributed to solving the Kepler conjecture by proving that the greatest packing density of spheres in three-dimensional space occurs when the centers of the spheres form a cubic face-centered arrangement. This was part of his review of Ludwig August Seeber's work on the theory of reduction of positive ternary quadratic forms. Gauss simplified Seeber's arguments, proved the central conjecture, and noted its equivalence to the Kepler conjecture for regular arrangements.
In two papers on biquadratic residues (1828, 1832), Gauss introduced the ring of Gaussian integers (Z[i]), demonstrating it is a unique factorization domain. He generalized key arithmetic concepts like Fermat's little theorem and Gauss's lemma. The primary goal was to formulate the law of biquadratic reciprocity, as he discovered that rings of complex integers provide the natural setting for such higher reciprocity laws. In the second paper, he stated the general law of biquadratic reciprocity and proved several special cases. An earlier 1818 publication, containing his fifth and sixth proofs of quadratic reciprocity, claimed that the techniques used (Gauss sums) could prove higher reciprocity laws.
3.1.2. Algebra
In his doctoral thesis from 1799, Gauss provided the first rigorous proof of the fundamental theorem of algebra, which states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. Prior to Gauss, mathematicians like Jean le Rond d'Alembert had offered incomplete or flawed proofs, and Gauss's dissertation included a critique of d'Alembert's work. He later produced three additional proofs, with the last one in 1849 generally considered fully rigorous. His efforts significantly clarified the concept of complex numbers.
3.1.3. Analysis
Gauss's work in analysis was pioneering, often anticipating later developments by decades. One of his early discoveries was the concept of the arithmetic-geometric mean (AGM) of two positive real numbers. In 1798-1799, he found its relation to elliptic integrals through Landen's transformation. A diary entry recorded the connection of Gauss's constant to lemniscatic elliptic functions, a result he believed "will surely open an entirely new field of analysis."
He also made early forays into the formal foundations of complex analysis. A letter to Bessel in 1811 indicates his knowledge of the "fundamental theorem of complex analysis"-Cauchy's integral theorem-and his understanding of complex residues when integrating around poles.
Euler's pentagonal numbers theorem, combined with his research on the AGM and lemniscatic functions, led him to numerous results on Jacobi theta functions. This culminated in his 1808 discovery of the Jacobi triple product identity, which includes Euler's theorem as a special case. His work shows he knew modular transformations of order 3, 5, and 7 for elliptic functions by 1808, anticipating later work by Legendre, Jacobi, and Ludwig Adolf Sohncke.
Several mathematical fragments in his Nachlass (posthumous papers) suggest he knew parts of the modern theory of modular forms. In his work on the multivalued AGM of two complex numbers, he discovered a deep connection between its infinitely many values and its two "simplest values." His unpublished writings include a sketch of the key concept of a fundamental domain for the modular group, such as a drawing of a tessellation of the unit disk by "equilateral" hyperbolic triangles.
Another example of Gauss's analytical insight is his cryptic remark in Disquisitiones Arithmeticae (article 335) that the principles of circle division by compass and straightedge could also apply to the division of the lemniscate curve, inspiring Abel's theorem on lemniscate division. His 1811 publication "Summatio quarundam serierum singularium" (on determining the sign of the quadratic Gauss sum) solved a major problem by introducing q-analogs of binomial coefficients and manipulating them with original identities, likely derived from his work on elliptic functions. However, Gauss presented his argument formally, without revealing its origin in elliptic functions theory.
In "Disquisitiones generales circa series infinitam..." (1813), Gauss provided the first systematic treatment of the general hypergeometric function (F(α,β,γ,x)), showing that many known functions were special cases. This work was the first in mathematics history to rigorously inquire into the convergence of infinite series. It also deals with infinite continued fractions arising as ratios of hypergeometric functions, now known as Gauss continued fractions.
In 1823, Gauss won a prize from the Danish Society for an essay on conformal mappings, which contained developments pertinent to complex analysis. He stated that angle-preserving mappings in the complex plane must be complex analytic functions and used the later-named Beltrami equation to prove the existence of isothermal coordinates on analytic surfaces. The essay concluded with examples of conformal mappings into a sphere and an ellipsoid of revolution.
3.1.4. Numeric analysis
Gauss often deduced theorems inductively from the numerical data he meticulously collected. Therefore, efficient algorithms were crucial to his research, and he made many contributions to numeric analysis, such as the method of Gaussian quadrature, published in 1816.
In a private letter to Gerling from 1823, Gauss described a solution for a 4x4 system of linear equations using the Gauss-Seidel method, an "indirect" iterative method for solving linear systems. He recommended it over the usual "direct elimination" for systems with more than two equations.
Gauss invented an algorithm for calculating what is now called discrete Fourier transforms (DFT) while calculating the orbits of Pallas and Juno in 1805, 160 years before James Cooley and John Tukey developed their similar Cooley-Tukey FFT algorithm. He developed it as a trigonometric interpolation method, but the paper Theoria Interpolationis Methodo Nova Tractata was published posthumously in 1876. This work was preceded by Joseph Fourier's first presentation on the subject in 1807.
3.1.5. Differential geometry
The geodetic survey of Hanover significantly fueled Gauss's interest in differential geometry and topology, fields concerned with curves and surfaces. This led to his 1828 publication of a memoir that is considered the birth of modern differential geometry of surfaces. This work departed from traditional methods of treating surfaces as Cartesian graphs of functions of two variables, instead initiating the exploration of surfaces from the "inner" perspective of a two-dimensional being constrained to move on it.
A key result from this work is the Theorema Egregium (Theorema Egregiumremarkable theoremLatin), which established a fundamental property of Gaussian curvature. Informally, the theorem states that the curvature of a surface can be determined entirely by measuring angles and distances on the surface itself, regardless of how the surface is embedded in three-dimensional space. The Theorema Egregium leads to the abstraction of surfaces as doubly-extended manifolds, clarifying the distinction between intrinsic properties (the metric) and extrinsic geometry. A practical consequence is the impossibility of an isometric transformation between surfaces with different Gaussian curvatures, meaning a sphere or ellipsoid cannot be flattened into a plane without distortion, a fundamental problem in map projections.
A significant portion of this essay is dedicated to a deep study of geodesics. Gauss proved the local Gauss-Bonnet theorem on geodesic triangles and generalized Legendre's theorem on spherical triangles to geodesic triangles on arbitrary surfaces with continuous curvature. He found that the angles of a "sufficiently small" geodesic triangle deviate from those of a planar triangle with the same sides in a way that depends only on the surface curvature at the triangle's vertices, not on the surface's behavior within the triangle's interior.
Gauss's 1828 memoir lacks the concept of geodesic curvature. However, an earlier, unpublished manuscript (likely 1822-1825) introduced the term "Seitenkrümmungside curvatureGerman" and proved its invariance under isometric transformations, a result later published by Ferdinand Minding in 1830. This paper also contains the core of his lemma on total curvature, and its generalization, later found and proved by Pierre Ossian Bonnet in 1848, known as the Gauss-Bonnet theorem.
3.1.6. Non-Euclidean geometry
During Gauss's lifetime, there was a lively debate surrounding the Parallel postulate in Euclidean geometry. Numerous attempts were made to prove it within the framework of Euclidean axioms, while some mathematicians explored the possibility of geometrical systems without it. Gauss pondered the fundamentals of geometry since the 1790s, realizing by the 1810s that a non-Euclidean geometry, independent of the parallel postulate, could exist without contradiction.
In a letter to Franz Taurinus in 1824, Gauss provided a concise outline of what he termed a "non-Euclidean geometryEnglish," but strictly forbade Taurinus from publishing it. Gauss is widely credited with being the first to discover and study non-Euclidean geometry, even coining the term. The first public publications on non-Euclidean geometry were by Nikolai Lobachevsky in 1829 and János Bolyai in 1832. Gauss continued to develop his ideas on the topic but chose not to publish them, thus avoiding influencing the ongoing scientific discussion.
Gauss commended János Bolyai's ideas in a letter to his father, Farkas Bolyai (Gauss's university friend), claiming they were congruent with his own thoughts from decades prior. However, the extent to which Gauss preceded Lobachevsky and Bolyai remains somewhat unclear due to the vague and obscure nature of his letter remarks. Sartorius first mentioned Gauss's work on non-Euclidean geometry in 1856, but Gauss's full ideas on the matter only became known with the posthumous publication of his papers in Volume VIII of his Collected Works (1900), by which time non-Euclidean geometry had already gained acceptance.
3.1.7. Topology
Gauss was an early pioneer in topology, or Geometria SitusGeometry of PositionLatin, as it was called in his era. His first proof of the fundamental theorem of algebra in 1799 contained an essentially topological argument, which he further developed in his fourth proof of the theorem fifty years later.

Another encounter with topological notions occurred during his astronomical work in 1804. He determined the limits of the region on the celestial sphere where comets and asteroids might appear, which he named "Zodiacus." He discovered that if the Earth's and a comet's orbits are linked, the Zodiacus encompasses the entire sphere due to topological reasons. In 1848, following the discovery of the asteroid 7 Iris, he published a further qualitative discussion of the Zodiacus.
In his letters from 1820-1830, Gauss intensively considered topics closely related to Geometria Situs, becoming increasingly aware of the semantic difficulties in this field. Fragments from this period reveal his attempts to classify "tract figures"-closed plane curves with a finite number of transverse self-intersections, which could also be planar projections of knots. To achieve this, he devised a symbolic scheme, the Gauss code, which captured the characteristic features of these figures.
In a fragment from 1833, Gauss defined the linking number of two space curves using a specific double integral, providing the first analytical formulation of a topological phenomenon. In the same note, he lamented the slow progress in Geometria Situs, remarking that one of its central problems would be "to count the intertwinings of two closed or infinite curves." His notebooks from that period also show his thoughts on other topological objects like braids and tangles.
Gauss's influence on the emerging field of topology, which he highly esteemed, was primarily through occasional remarks and oral communications to students like Möbius and Listing.
3.1.8. Theory of errors
Gauss likely employed the method of least squares for calculating the orbit of Ceres to minimize the impact of measurement error. While Adrien-Marie Legendre published the method first in 1805, Gauss claimed in Theoria motus (1809) that he had been using it since 1794 or 1795. This disagreement is known as the "priority dispute over the discovery of the method of least squares" in the history of statistics.
Gauss proved that the method of least squares yields the lowest sampling variance within the class of linear unbiased estimators, assuming normally distributed errors (the Gauss-Markov theorem). He presented this in his two-part paper Theoria combinationis observationum erroribus minimis obnoxiae (1823). In the first part, he proved Gauss's inequality (a Chebyshev-type inequality) for unimodal distributions and stated, without proof, another inequality for moments of the fourth order (a special case of Gauss-Winckler inequality). He also derived lower and upper bounds for the variance of sample variance. The second part described recursive least squares methods. His work on error theory was further extended by geodesist Friedrich Robert Helmert into the Gauss-Helmert model.
Gauss also contributed to problems in probability theory not directly related to error theory. For instance, a diary note shows his attempt to describe the asymptotic distribution of entries in the continued fraction expansion of a random number uniformly distributed in (0,1). He derived this distribution, now known as the Gauss-Kuzmin distribution, as a byproduct of discovering the ergodicity of the Gauss map for continued fractions. Gauss's solution represents the first result in the metrical theory of continued fractions.
3.1.9. Minor mathematical accomplishments
Gauss applied the concept of complex numbers to solve well-known problems in new, concise ways. For example, in a short note from 1836 on geometric aspects of ternary forms and their application to crystallography, he stated the fundamental theorem of axonometry, which explains how to represent a 3D cube on a 2D plane with complete accuracy using complex numbers. He described rotations of this sphere as the action of certain linear fractional transformations on the extended complex plane. He also provided a proof for the geometric theorem that the altitudes of a triangle always meet in a single orthocenter.
Gauss was concerned with John Napier's "Pentagramma mirificum"-a specific spherical pentagram-for several decades, approaching it from various perspectives and gradually gaining a full understanding of its geometric, algebraic, and analytic aspects. In 1843, he stated and proved several theorems connecting elliptic functions, Napier spherical pentagons, and Poncelet pentagons in the plane.
Furthermore, he contributed a solution to the problem of constructing the largest-area ellipse inside a given quadrilateral and discovered a surprising result about the computation of the area of pentagons.
3.2. Astronomy
Gauss's astronomical work was crucial in establishing his scientific reputation and led to significant developments in orbital mechanics and geodesy.
3.2.1. Discovery of Ceres and orbital mechanics

On 1 January 1801, Italian astronomer Giuseppe Piazzi discovered a new celestial object, which he presumed to be the long-sought planet between Mars and Jupiter, as predicted by the Titius-Bode law. Piazzi named it Ceres. He could only track it for a short period before it disappeared behind the glare of the Sun. The mathematical tools available at the time were insufficient to extrapolate a position for its reappearance from the limited data.
Gauss, then 23, tackled this problem. After three months of intense work, he predicted a position for its possible rediscovery in December 1801. This prediction proved accurate within half a degree when Franz Xaver von Zach at Gotha Observatory on 7 and 31 December, and independently Heinrich Wilhelm Matthäus Olbers in Bremen on 1 and 2 January, identified the object near the predicted position. Zach stated that without Gauss's intellectual work and calculations, Ceres could not have been rediscovered.
Gauss's method for this calculation led to an eighth-degree equation, of which one solution (Earth's orbit) was known. The desired solution was then separated from the remaining six based on physical conditions. For this work, Gauss developed comprehensive approximation methods.
The successful prediction of Ceres's orbit led Gauss to develop a theory for the motion of planetoids disturbed by large planets, which he published in 1809 as Theoria motus corporum coelestium in sectionibus conicis solem ambientum. This work introduced the Gaussian gravitational constant and formalized the method of least squares, which he had been using since 1795.
3.2.2. Perturbation theory
Following the discovery of new asteroids, Gauss focused on the perturbations of their orbital elements. Initially, he analyzed Ceres using analytical methods similar to Laplace's. However, his preferred object was Pallas due to its high eccentricity and orbital inclination, which rendered Laplace's method ineffective. Gauss applied his own tools, including the arithmetic-geometric mean, the hypergeometric function, and his interpolation method.
In 1812, he identified an orbital resonance with Jupiter in an 18:7 ratio, which he initially communicated as a cipher, later revealing its meaning in letters to Olbers and Bessel. After years of work, he concluded his research on Pallas in 1816 without a result he deemed sufficient, marking the end of his activities in theoretical astronomy.
One outcome of Gauss's research on Pallas perturbations was Determinatio Attractionis... (1818), a work on theoretical astronomy that introduced the "elliptic ring method." This method involved an averaging concept where a planet in orbit is replaced by a fictitious ring with a mass density proportional to the time taken for the planet to traverse corresponding orbital arcs. Gauss presented a method for evaluating the gravitational attraction of such an elliptic ring, which included a direct application of the arithmetic-geometric mean (AGM) algorithm to calculate an elliptic integral.
3.2.3. Geodetic survey and arc measurement


Gauss had been involved with geodetic problems since 1799, when he assisted Karl Ludwig von Lecoq with calculations during his survey in Westphalia. From 1804, he self-taught practical geodesy using a sextant in Brunswick and Göttingen.
In 1816, Gauss's former student Heinrich Christian Schumacher, then a professor in Copenhagen and head of an observatory in Altona (Holstein), was conducting a triangulation of the Jutland peninsula. This project aimed to produce maps and determine the geodetic arc between terminal sites, which would provide more precise results for determining Earth's geoid dimensions. Schumacher asked Gauss to extend this work southward into the Kingdom of Hanover, and Gauss agreed. In May 1820, King George IV formally ordered Gauss to undertake the project.
An arc measurement requires precise astronomical determination of at least two points in the network. Gauss and Schumacher utilized the fact that their observatories in Göttingen and Altona were nearly on the same longitude. They measured latitude using their instruments and a zenith sector by Jesse Ramsden, which had previously been used in the Principal Triangulation of Great Britain and was transported between both observatories.
Gauss and Schumacher had already determined angles between Lüneburg, Hamburg, and Lauenburg in October 1818 for geodetic connection. From 1821 to 1825, Gauss personally directed the triangulation work, extending from Thuringia in the south to the Elbe river in the north. The largest triangle he measured, between Hoher Hagen, Großer Inselsberg in the Thuringian Forest, and Brocken in the Harz mountains, had a maximum side length of 66 mile (107 km). In the sparsely populated Lüneburg Heath, where natural summits were scarce, he sometimes had to cut lanes through vegetation to find suitable triangulation points.
For signaling, Gauss invented the heliotrope, an instrument with movable mirrors and a small telescope that reflected sunbeams to triangulation points. He also created a "vice heliotrope," a sextant with an additional mirror. Soldiers from the Hanoverian army, including his eldest son Joseph, assisted him. Gauss participated in Schumacher's baseline measurement (Braak Base Line) in Braak near Hamburg in 1820, using the results to evaluate the Hanoverian triangulation.
An additional outcome was an improved value for the flattening of the approximate Earth ellipsoid, refining Walbeck's 1820 value of 1/302.78 to 1/298.39. Gauss developed the universal transverse Mercator projection (which he called conform projection) for representing geodetic data on plane charts.
After completing the arc measurement, Gauss began extending the triangulation westward to survey the entire Kingdom of Hanover, following a Royal decree from 25 March 1828. Three army officers, including Lieutenant Joseph Gauss, directed the practical work. Gauss himself handled the complete data evaluation, applying his mathematical inventions like the method of least squares and the elimination method. The project concluded in 1844, with Gauss submitting a final report; his projection method was not published until 1866.
In 1828, while studying latitude differences, Gauss first defined a physical approximation for the figure of the Earth as the surface everywhere perpendicular to the direction of gravity. His doctoral student Johann Benedict Listing later termed this the geoid.
3.2.4. Observational astronomy
While Gauss's contributions to theoretical astronomy diminished, his practical activities in observational astronomy continued throughout his career. As early as 1799, he worked on determining longitude using lunar parallax, developing more convenient formulas than those in common use. Upon becoming observatory director, he emphasized fundamental astronomical constants in his correspondence with Bessel. Gauss himself provided tables for nutation, aberration, solar coordinates, and refraction. He made many contributions to spherical geometry and solved practical problems related to navigation by stars. He published numerous observations, mainly on minor planets and comets; his last recorded observation was the solar eclipse of 28 July 1851.
3.3. Physics
Gauss's influential contributions extended to various branches of physics, particularly in electromagnetism and potential theory.
3.3.1. Geomagnetism


Gauss's interest in magnetism dated back to 1803. After Alexander von Humboldt visited Göttingen in 1826, both scientists began intensive research on geomagnetism, sometimes independently, sometimes in productive cooperation. In 1828, Gauss attended the Society of German Natural Scientists and Physicians conference in Berlin as Humboldt's guest, where he met physicist Wilhelm Eduard Weber.
When Weber became the chair for physics in Göttingen in 1831, succeeding Johann Tobias Mayer through Gauss's recommendation, they began a fruitful collaboration. Their work led to new insights into magnetism, including a representation for the unit of magnetism in terms of mass, charge, and time. They founded the Magnetischer VereinMagnetic AssociationGerman, an international working group of several observatories. This association supported synchronized measurements of Earth's magnetic field in many regions worldwide from 1836 to 1841.
In 1836, Humboldt suggested establishing a global network of geomagnetic stations in British dominions to the Duke of Sussex, then president of the Royal Society. He proposed standardized magnetic measurements using his methods. This initiative, along with others, led to a global program known as the "Magnetical crusade" under Edward Sabine. Observation dates, times, and intervals were predetermined, with Göttingen mean time serving as the standard. Sixty-one stations across all five continents participated, and Gauss and Weber edited six volumes of published results between 1837 and 1843. Weber's departure to Leipzig in 1843, a consequence of the Göttingen Seven affair, marked the end of the Magnetic Association's activities.
Following Humboldt's example, Gauss ordered a magnetic observatory to be built in the garden of the astronomical observatory. However, they differed on instrumentation: Gauss preferred stationary instruments for precision, while Humboldt favored movable ones. Gauss was interested in the temporal and spatial variation of magnetic declination, inclination, and intensity. Together with Weber, he developed methods to measure the components of the magnetic field's intensity and constructed a suitable magnetometer to measure absolute values of Earth's magnetic field strength, rather than just relative ones. This work marked the first time a non-mechanical quantity was derived from basic mechanical quantities, with the magnetometer's precision being about ten times higher than previous instruments.
Gauss published a General Theory of Terrestrial Magnetism (1839), which he believed described the nature of magnetic force. According to Felix Klein, this work was more a presentation of observations using spherical harmonics than a physical theory. The theory predicted the existence of exactly two magnetic poles on Earth, rendering Christopher Hansteen's idea of four magnetic poles obsolete, and allowed for their location to be determined with good precision.
Gauss influenced the beginning of geophysics in Russia, as his former students Adolph Theodor Kupffer and Ivan Simonov founded magnetic observatories in St. Petersburg and Kazan, respectively, following the Göttingen model.
3.3.2. Electromagnetism
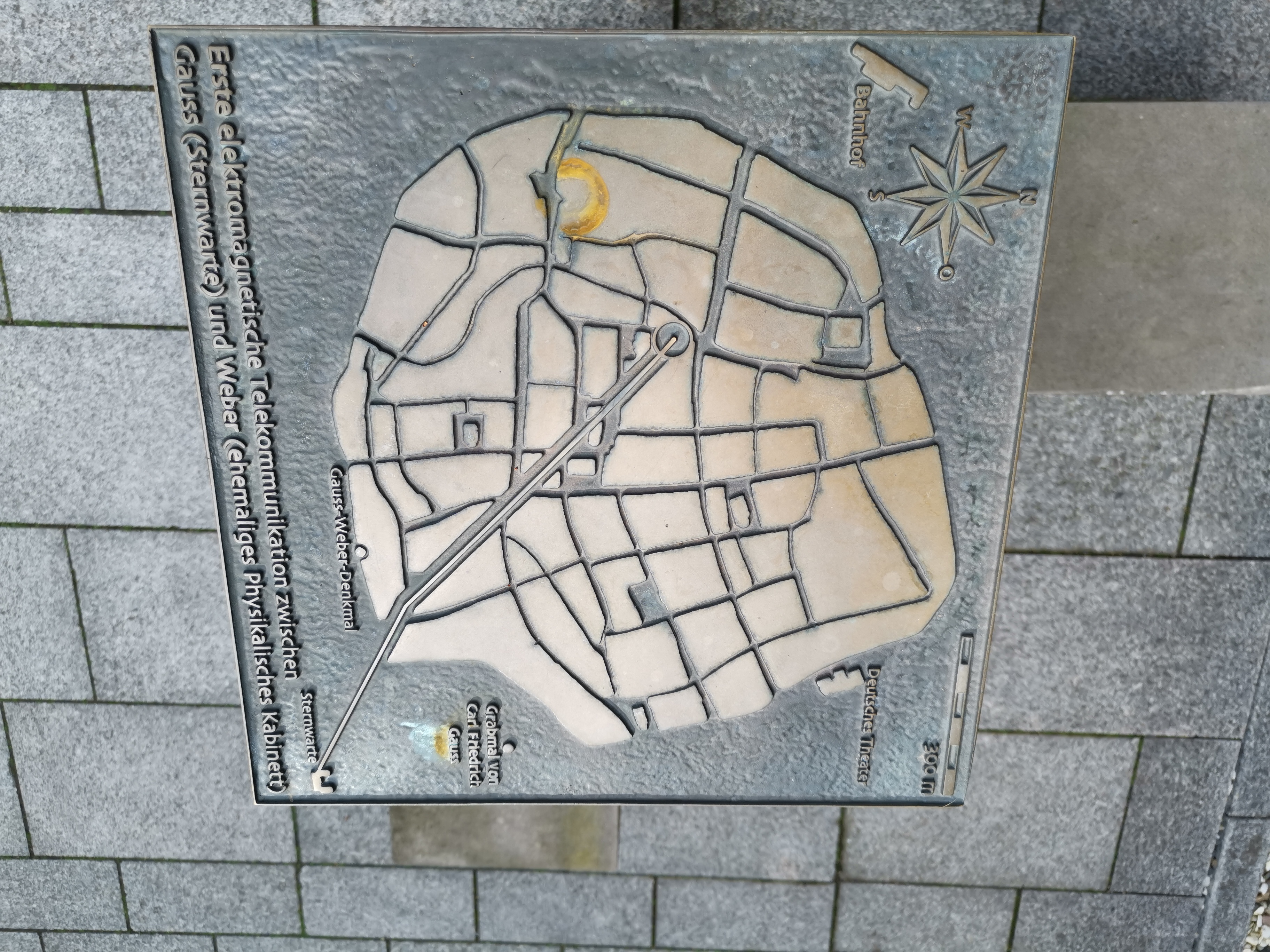
The discoveries of Hans Christian Ørsted on electromagnetism and Michael Faraday on electromagnetic induction drew Gauss's attention. Gauss and Weber formulated rules for branched electric circuits, later independently discovered and published by Gustav Kirchhoff as Kirchhoff's circuit laws. They also conducted inquiries into electromagnetism. In 1833, they constructed the first electromechanical telegraph, with Weber connecting the observatory to the physics institute in Göttingen's town center, though the cable was damaged by a thunderstorm in 1845. However, they did not pursue commercial development of this invention.
Gauss's main theoretical interest in electromagnetism was to formulate quantitative laws for electromagnetic induction. His notebooks from these years contain several innovative formulations; he discovered the idea of a vector potential function (independently rediscovered by Franz Ernst Neumann in 1845). In January 1835, he wrote down an "induction law" equivalent to Faraday's law, stating that the electromotive force at a given point in space equals the instantaneous rate of change (with respect to time) of this function.
Gauss attempted to find a unifying law for long-distance effects of electrostatics, electrodynamics, electromagnetism, and induction, similar to Newton's law of gravitation, but this endeavor ultimately ended in what has been described as a "tragic failure."
3.3.3. Potential theory
Since Isaac Newton had theoretically shown that Earth and rotating stars assume non-spherical shapes, the problem of attraction of ellipsoids gained importance in mathematical astronomy. In his first publication on potential theory, "Theoria attractionis..." (1813), Gauss provided a closed-form expression for the gravitational attraction of a homogeneous triaxial ellipsoid at every point in space. Unlike previous research by Maclaurin, Laplace, and Lagrange, Gauss's new solution treated the attraction more directly as an elliptic integral. In this process, he also proved and applied some special cases of the Gauss's theorem in vector analysis.
In the General theorems concerning the attractive and repulsive forces acting in reciprocal proportions of quadratic distances (1840), Gauss laid the groundwork for a theory of the magnetic potential, building on the work of Lagrange, Laplace, and Poisson. It is unlikely he was aware of George Green's earlier work on this subject. However, Gauss was never able to provide a comprehensive theory of magnetism comparable to Newton's work on gravitation, one that would enable scientists to predict future geomagnetic effects.
3.3.4. Optics
Gauss's calculations enabled instrument maker Johann Georg Repsold in Hamburg to construct a new achromatic lens system in 1810. A significant challenge was the imprecise knowledge of the refractive index and dispersion of the glass types used. In a short article from 1817, Gauss addressed the problem of removing chromatic aberration in double lenses, computing adjustments for shape and refraction coefficients to minimize it. His work was recognized by optician Carl August von Steinheil, who in 1860 introduced the achromatic Steinheil doublet, partly based on Gauss's calculations. Many of Gauss's results in geometrical optics are scattered in his correspondences and handwritten notes.
In the Dioptrical Investigations (1840), Gauss provided the first systematic analysis of image formation under a paraxial approximation (Gaussian optics). He characterized optical systems under this approximation solely by their cardinal points, and he derived the Gaussian lens formula, applicable without restrictions regarding lens thickness.
3.3.5. Mechanics
Gauss's initial work in mechanics concerned the earth's rotation. When his university friend Johann Benzenberg conducted experiments in 1802 to determine the deviation of falling masses from the perpendicular (an effect now known as the Coriolis force), he asked Gauss for a theoretical calculation to compare with his experimental data. Gauss developed a system of fundamental equations for the motion, and his results sufficiently corresponded with Benzenberg's data, which were included as an appendix to Benzenberg's book on falling experiments.
After Léon Foucault publicly demonstrated Earth's rotation with his Foucault pendulum experiment in 1851, Gerling questioned Gauss for further explanations. This prompted Gauss to design a new apparatus for demonstration, using a much shorter pendulum than Foucault's. The oscillations were observed with a reading telescope, a vertical scale, and a mirror attached to the pendulum. This apparatus is described in the Gauss-Gerling correspondence, and Weber conducted some experiments with it in 1853, though no data were published.
Gauss's principle of least constraint (1829) was established as a general concept to unify statics and dynamics in mechanics, combining D'Alembert's principle with Lagrange's principle of virtual work, and showing analogies to the method of least squares.
3.3.6. Metrology
In 1828, Gauss was appointed head of a Board for weights and measures in the Kingdom of Hanover. He oversaw the creation of standards for length and measures. Gauss personally handled the time-consuming measurements and provided detailed instructions for mechanical preparation. In his correspondence with Schumacher, who was also working on this matter, he described new ideas for high-precision scales. He submitted the final reports on the Hanoverian foot and pound to the government in 1841. This work gained more than regional importance through a law enacted in 1836 that linked Hanoverian measures with English ones, demonstrating the practical application of scientific rigor to societal needs.
4. Honours and awards

Gauss received his first membership in a scientific society in 1802 from the Russian Academy of Sciences. He was subsequently awarded numerous memberships (corresponding, foreign, or full) from prestigious institutions worldwide, reflecting his widespread international recognition. These included:
- Academy of Sciences in Göttingen (1802/1807)
- French Academy of Sciences (1804/1820)
- Royal Society of London (1804)
- Royal Prussian Academy in Berlin (1810)
- National Academy of Science in Verona (1810)
- Royal Society of Edinburgh (1820)
- Bavarian Academy of Sciences of Munich (1820)
- Royal Danish Academy in Copenhagen (1821)
- Royal Astronomical Society in London (1821)
- Royal Swedish Academy of Sciences (1821)
- American Academy of Arts and Sciences in Boston (1822)
- Royal Bohemian Society of Sciences in Prague (1833)
- Royal Academy of Science, Letters and Fine Arts of Belgium (1841/1845)
- Royal Society of Sciences in Uppsala (1843)
- Royal Irish Academy in Dublin (1843)
- Royal Institute of the Netherlands (1845/1851)
- Spanish Royal Academy of Sciences in Madrid (1850)
- Russian Geographical Society (1851)
- Imperial Academy of Sciences in Vienna (1848)
- American Philosophical Society (1853)
- Cambridge Philosophical Society
- Royal Hollandish Society of Sciences in Haarlem
Both the University of Kazan and the Philosophy Faculty of the University of Prague appointed him honorary member in 1848.
Gauss received several prestigious awards for his scientific achievements:
- The Lalande Prize from the French Academy of Science in 1809 for his theory of planets and methods for determining their orbits from only three observations.
- The Danish Academy of Science prize in 1823 for his memoir on conformal projection.
- The Copley Medal from the Royal Society in 1838 for "his inventions and mathematical researches in magnetism."
He was also recognized with various national and royal orders:
- Knight of the French Legion of Honour in 1837.
- One of the first members of the Prussian Order Pour le Merite (Civil class) when it was established in 1842.
- The Order of the Crown of Westphalia (1810).
- The Danish Order of the Dannebrog (1817).
- The Hanoverian Royal Guelphic Order (1815).
- The Swedish Order of the Polar Star (1844).
- The Order of Henry the Lion (1849).
- The Bavarian Maximilian Order for Science and Art (1853).
The Kings of Hanover bestowed upon him the honorary titles "Hofrath" (Court Councillor) in 1816 and "Geheimer Hofrath" (Secret Court Councillor) in 1845. In 1849, on the occasion of his golden doctor degree jubilee, he was granted honorary citizenship by both Brunswick and Göttingen. Soon after his death, King George V of Hanover ordered a medal to be issued with the inscription "to the Prince of Mathematicians" dedicated to Gauss.
The "Gauss-Gesellschaft Göttingen" (Göttingen Gauss Society) was founded in 1964 to research the life and work of Carl Friedrich Gauss and related persons, publishing the Mitteilungen der Gauss-Gesellschaft (Communications of the Gauss Society).
5. Selected writings
Gauss's published works, though fewer than his private discoveries, were seminal and had a lasting impact on mathematics and physics. His extensive correspondence also provides valuable insights into his scientific process and collaborations.
5.1. Mathematics and astronomy

- 1799: Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse (Doctoral thesis on the fundamental theorem of algebra, University of Helmstedt)
- 1800: Berechnung des Osterfestes (Calculation of Easter)
- 1801: Disquisitiones Arithmeticae (Investigations in Arithmetic)
- 1802: Berechnung des jüdischen Osterfestes (Calculation of Jewish Easter)
- 1804: Über die Grenzen der geocentrischen Oerter der Planeten (On the limits of the geocentric places of the planets, on the Zodiacus)
- 1808: Theorematis arithmetici demonstratio nova (New proof of an arithmetic theorem, introduces Gauss's lemma, uses it in the third proof of quadratic reciprocity)
- 1808: Methodus peculiaris elevationem poli determinandi (A special method for determining the elevation of the pole)
- 1809: Theoria motus corporum coelestium in sectionibus conicis solem ambientium (Theory of the Motion of Heavenly Bodies Moving about the Sun in Conic Sections)
- 1811: Disquisitio de elementis ellipticis Palladis ex oppositionibus annorum 1803, 1804, 1805, 1806, 1807, 1808, 1809 (Orbit of Pallas)
- 1811: Summatio quarundam serierum singularium (Summation of certain singular series, from 1808; determines the sign of the quadratic Gauss sum, uses this for the fourth proof of quadratic reciprocity)
- 1813: Disquisitiones generales circa seriem infinitam 1 + αβ/γ + ... (from 1812, contains the Gauss's continued fraction)
- 1816: Methodus nova integralium valores per approximationem inveniendi (New method for finding the values of integrals by approximation, from 1814)
- 1816: Demonstratio nova altera theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse (Second new proof of the theorem that every integral algebraic function of one variable can be resolved into real factors of the first or second degree)
- 1816: Theorematis de resolubilitate functionum algebraicarum integrarum in factores reales demonstratio tertia (Third demonstration of the theorem on the resolvability of integral algebraic functions into real factors)
- 1818: Theorematis fundamentalis in doctrina de residuis quadraticis demonstrationes et ampliationes novae (New demonstrations and amplifications of the fundamental theorem in the doctrine of quadratic residues, from 1817; fifth and sixth proofs of quadratic reciprocity)
- 1818: Determinatio attractionis, quam in punctum positionis datae exerceret planeta, si eius massa per totamorbitam, ratione temporis, quo singulae partes describuntur, uniformiter esset dispertita (Determination of the attraction which a planet would exert on a given point of position, if its mass were uniformly distributed over the whole orbit, in proportion to the time in which the individual parts are described; only reference to the - mostly unpublished - work on the algorithm of the arithmetic-geometric mean)
- 1823: Theoria combinationis observationum erroribus minimis obnoxiae. Pars Prior (Theory of the combination of observations most liable to minimum errors. Part One, from 1821)
- 1823: Theoria combinationis observationum erroribus minimis obnoxiae. Pars Posterior (Theory of the combination of observations most liable to minimum errors. Part Two)
- 1825: Allgemeine Auflösung der Aufgabe die Theile einer gegebnen Fläche auf einer andern gegebnen Fläche so abzubilden dass die Abbildung dem Abgebildeten in den kleinsten Theilen ähnlich wird (General solution of the problem of mapping parts of a given surface onto another given surface such that the mapping is similar to the mapped in the smallest parts; prize-winning essay from 1822 on conformal mapping)
- 1828: Bestimmung des Breitenunterschiedes zwischen den Sternwarten von Göttingen und Altona durch Beobachtungen am Ramsdenschen Zenithsector (Determination of the Difference in Latitude between the Observatories of Göttingen and Altona by Observations with Ramsden's Zenith sector)
- 1828: Supplementum theoriae combinationis observationum erroribus minimis obnoxiae (Supplement to the theory of the combination of observations most liable to minimum errors, from 1826)
- 1828: Disquisitiones generales circa superficies curvas (General investigations of curved surfaces, from 1827)
- 1828: Theoria residuorum biquadraticorum, Commentatio prima (Theory of biquadratic residues, First commentary, from 1825)
- 1832: Theoria residuorum biquadraticorum, Commentatio secunda (Theory of biquadratic residues, Second commentary, from 1831; introduces the Gaussian integers, states (without proof) the law of biquadratic reciprocity, proves the supplementary law for 1 + i)
- 1845: Untersuchungen über Gegenstände der Höheren Geodäsie. Erste Abhandlung (Investigations on subjects of higher geodesy. First treatise, from 1843)
- 1847: Untersuchungen über Gegenstände der Höheren Geodäsie. Zweite Abhandlung (Investigations on subjects of higher geodesy. Second treatise, from 1846)
- 1848: Schreiben des Herrn Geheimen Hofrathes Gauss an den Herausgeber (Letter of Mr. Secret Councillor of the Court Gauss to the editor, on the Zodiacus)
- 1850: Beiträge zur Theorie der algebraischen Gleichungen (Contributions to the theory of algebraic equations; lecture from 1849)
- 1903: Wissenschaftliches Tagebuch (Scientific Diary, 1796-1814)
5.2. Physics
- 1804: Fundamentalgleichungen für die Bewegung schwerer Körper auf der Erde (Fundamental equations for the motion of heavy bodies on Earth, in Benzenberg's book Versuche über das Gesetz des Falls, über den Widerstand der Luft und über die Umdrehung der Erde)
- 1813: Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata (Theory of the attraction of homogeneous spheroidal elliptic bodies treated by a new method; contains Gauss's theorem of vector analysis)
- 1817: Ueber die achromatischen Doppelobjective besonders in Rücksicht der vollkommnern Aufhebung der Farbenzerstreuung (On achromatic double lenses with special regard to a more complete dispersion of colors)
- 1829: Über ein neues allgemeines Grundgesetz der Mechanik (On a new General Fundamental Law of Mechanics)
- 1830: Principia generalia theoriae figurae fluidorum in statu aequilibrii (General principles of the theory of the figure of fluids in a state of equilibrium, from 1829)
- 1836: Erdmagnetismus und Magnetometer (Terrestrial Magnetism and Magnetometer)
- 1840: Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnis des Quadrats der Entfernung wirkenden Anziehungs- und Abstoßungskräfte (General Theorems concerning the attractive and repulsive Forces acting in reciprocal Proportions of quadratic Distances)
- 1841: Intensitas vis magneticae terrestris ad mensuram absolutam revocata (The Intensity of the Earth's Magnetic Force Reduced to Absolute Measurement, from 1832)
- 1843: Dioptrische Untersuchungen (Dioptrical Investigations, from 1840)
5.2.1. Together with Wilhelm Weber
- 1837-1839: Resultate aus den Beobachtungen des magnetischen Vereins im Jahre 1836-1838 (Results from the observations of the Magnetic Association in the years 1836-1838)
- 1840-1843: Resultate aus den Beobachtungen des magnetischen Vereins im Jahre 1839-1841 (Results from the observations of the Magnetic Association in the years 1839-1841)
- 1840: Atlas des Erdmagnetismus nach den Elementen der Theorie entworfen. Supplement zu den Resultaten aus den Beobachtungen des magnetischen Vereins (Atlas of Terrestrial Magnetism designed according to the elements of the theory. Supplement to the results from the observations of the Magnetic Association)
5.3. Collected works
- Carl Friedrich Gauss. Werke (Carl Friedrich Gauss. Works), volumes 1-12, edited by the Royal Prussian Academy of Sciences (1863-1933). This collection includes his unpublished literary estate.
5.4. Correspondence
Gauss's extensive correspondence offers unique insights into his scientific process, collaborations, and personal relationships. The Göttingen Academy of Sciences and Humanities provides a complete online collection of his known letters. His literary estate is preserved by the Göttingen State and University Library, and additional materials can be found in the municipal archive of Brunswick.
Notable correspondences include:
- Letters between Gauss and Friedrich Wilhelm Bessel (December 1804 to August 1844)
- Letters to Palm Heinrich Ludwig von Boguslawski (February 1835 to January 1848)
- Letters between Gauss and Johann Elert Bode (February 1802 to October 1826)
- Letters between Carl Friedrich Gauss and Farkas Bolyai (September 1797 to February 1853)
- Letters between Carl Friedrich Gauss and Johann Franz Encke (June 1810 to June 1854)
- Letters between Carl Friedrich Gauss and Christian Ludwig Gerling (June 1810 to June 1854)
- Letters between Alexander von Humboldt and Gauss (July 1807 to December 1854)
- Letters between Carl Friedrich Gauss and Karl Kreil (1835 to 1843)
- Letters between Carl Friedrich Gauss and Karl Ludwig von Lecoq (February 1799 to September 1800)
- The correspondence between Carl Friedrich Gauss and the Rev. Nevil Maskelyne (1802-1805)
- Letters between Wilhelm Olbers and Gauss (January 1802 to May 1839)
- Letters between C. F. Gauss and Heinrich Christian Schumacher (April 1808 to November 1850)
- Letters between Carl Friedrich Gauss and Eberhard August Wilhelm von Zimmermann (1795 to 1815)
6. Commemorations
Carl Friedrich Gauss's profound impact on science and culture has been honored in numerous ways:
- Currency and Stamps:** From 1989 to 2001, Gauss's portrait, along with a Gaussian distribution curve and famous Göttingen buildings, was featured on the German 10-Deutsche Mark banknote. The reverse side depicted his favorite sextant and a map of the Kingdom of Hanover. Germany has also issued three postage stamps in his honor: one in 1955 marking the centenary of his death, and two in 1977 celebrating his 200th birthday.
- Prizes and Institutions:** In 2002, the International Mathematical Union and the German Mathematical Society jointly established the Carl Friedrich Gauss Prize, one of the most prestigious awards in mathematics, to commemorate his legacy. The "Gauss-Gesellschaft Göttingen" (Göttingen Gauss Society), founded in 1964, is dedicated to researching his life and work.
- Monuments and Memorials:** A statue of Gauss, created by Hermann Heinrich Howaldt and designed by Fritz Schaper, was erected in his birthplace, Brunswick, in 1880. In 2007, a portrait bust of Gauss was placed in the Walhalla memorial.
- Cultural References:** The 2005 novel Die Vermessung der Welt (Die Vermessung der WeltMeasuring the WorldGerman) by Daniel Kehlmann, later adapted into a 2012 film by Detlev Buck, explores Gauss's life and work through a historical fiction lens, contrasting him with German explorer Alexander von Humboldt.
- Scientific and Geographical Naming:** Numerous scientific concepts, theorems, units, and geographical features are named after Gauss, reflecting his pervasive influence across disciplines. For a comprehensive list, see List of things named after Carl Friedrich Gauss.
- Digital Commemorations:** On 30 April 2018, Google honored Gauss on his 241st birthday with a Google Doodle displayed in various parts of the world.
- Academic Tributes:** In 1929, Polish mathematician Marian Rejewski, who later helped break the Enigma machine code, placed flowers on Gauss's grave in Göttingen at the request of his professor, Zdzisław Krygowski.
7. Further reading
For those interested in delving deeper into the life and scientific contributions of Carl Friedrich Gauss, the following resources are recommended:
- Boyer, Carl B., and Uta C. Merzbach. A History of Mathematics. 3rd ed. John Wiley & Sons, 2011.
- Bühler, Walter Kaufmann. Gauss: A Biographical Study. Springer-Verlag, 1987.
- Dunnington, G. Waldo. Carl Friedrich Gauss: Titan of Science. The Mathematical Association of America, 2004.
- Hall, Tord. Carl Friedrich Gauss: A Biography. MIT Press, 1970.
- Kehlmann, Daniel. Measuring the World. Translated by Carol Brown Janeway. Pantheon, 2006. (Original German: Die Vermessung der Welt, 2005)
- Nahin, Paul J. An Imaginary Tale: The Story of √-1. Princeton University Press, 2010.
- Sartorius von Waltershausen, Wolfgang. Gauss: A Memorial. Translated by Helen Worthington Gauss. Colorado Springs, 1966. (Original German: Gauss zum Gedächtniss, 1856)
- Simmons, J. The Giant Book of Scientists: The 100 Greatest Minds of All Time. The Book Company, 1996.
- Tent, Margaret. The Prince of Mathematics: Carl Friedrich Gauss. A. K. Peters, 2006.
8. See also
- List of things named after Carl Friedrich Gauss
- History of mathematics
- History of physics
- History of astronomy
- Normal distribution
- Fundamental theorem of algebra
- Disquisitiones Arithmeticae
- Theoria motus corporum coelestium
- Theorema Egregium
- Non-Euclidean geometry
- Geomagnetism
- Electromagnetic telegraph
- Method of least squares
- Gauss (unit)